Course Description
In this course, we will cover some mathematical principles that are important for RF and communications engineering.
The topics covered include:
- Algebra, equations, quadratics, logs, dB, triangles, trigonometry, and units.
- Vector fundamentals, spherical coordinates, dot and cross products.
- Basics of complex numbers, Euler's Formula, complex number arithmetic.
- Fourier transform concepts.
- Spherical trigonometry fundamentals.
Included with the course are a Quick Reference Guide, containing all formulas and constants, plus access to the SatProf Toolkit desktop app which contains RF calculators and single- and dual-segment link budget simulators.
Audience:
This course is recommended for technicians, engineers, and anyone wishing to reinforce their math knowledge for working with satellite communications and any other microwave/RF links and systems.
Prerequisites:
If you had these topics in high school or university, these lessons will be a review. If you have not seen these topics before and you are having trouble with this lesson, there are many excellent textbooks and Internet resources which can help answer your questions or explain the topics in depth and in different ways.
Delivery:
Animated & interactive HTML5, self-paced, on-line format. Requirements: internet access while studying the course material (high speed preferred ); current browser with JavaScript enabled; permission to access SatProf server and learning system websites; mouse.
Tests:
Each lesson contains a mandatory quiz. All pages must be viewed and all quizzes must be passed in order to satisfactorily complete the course.Lessons Included
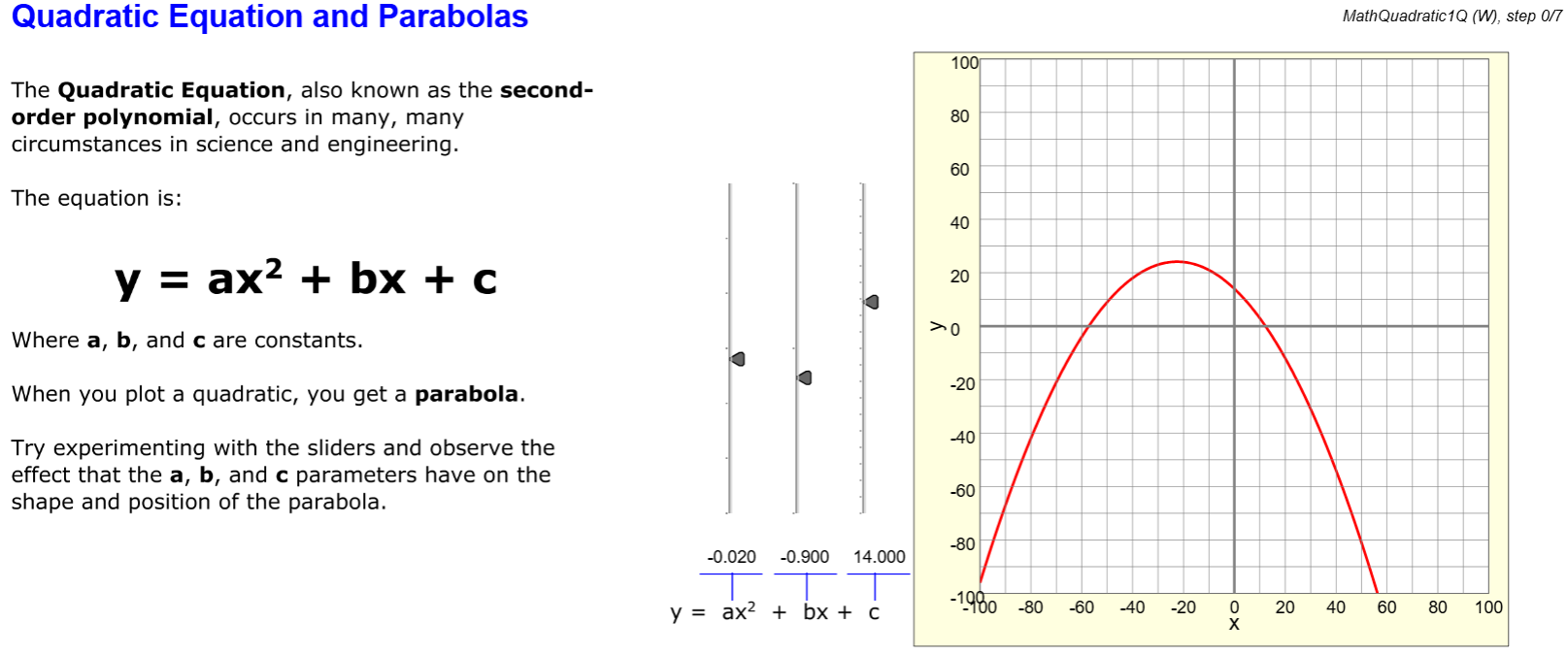
- Algebra, Logs, and Trigonometry
In this lesson we will review: Algebra: rearranging equations, solving simultaneous equations. Linear equations; fitting an equation to two points. The quadratic equation and parabolas. Working with logarithms and exponentials, deciBels (dB), and power ratios. Triangles and Pythagoras's theorem. Trigonometry basics: radians and degrees; sines, cosines, and tangents, and their inverses. Using metrix prefixes to SI units in engineering.
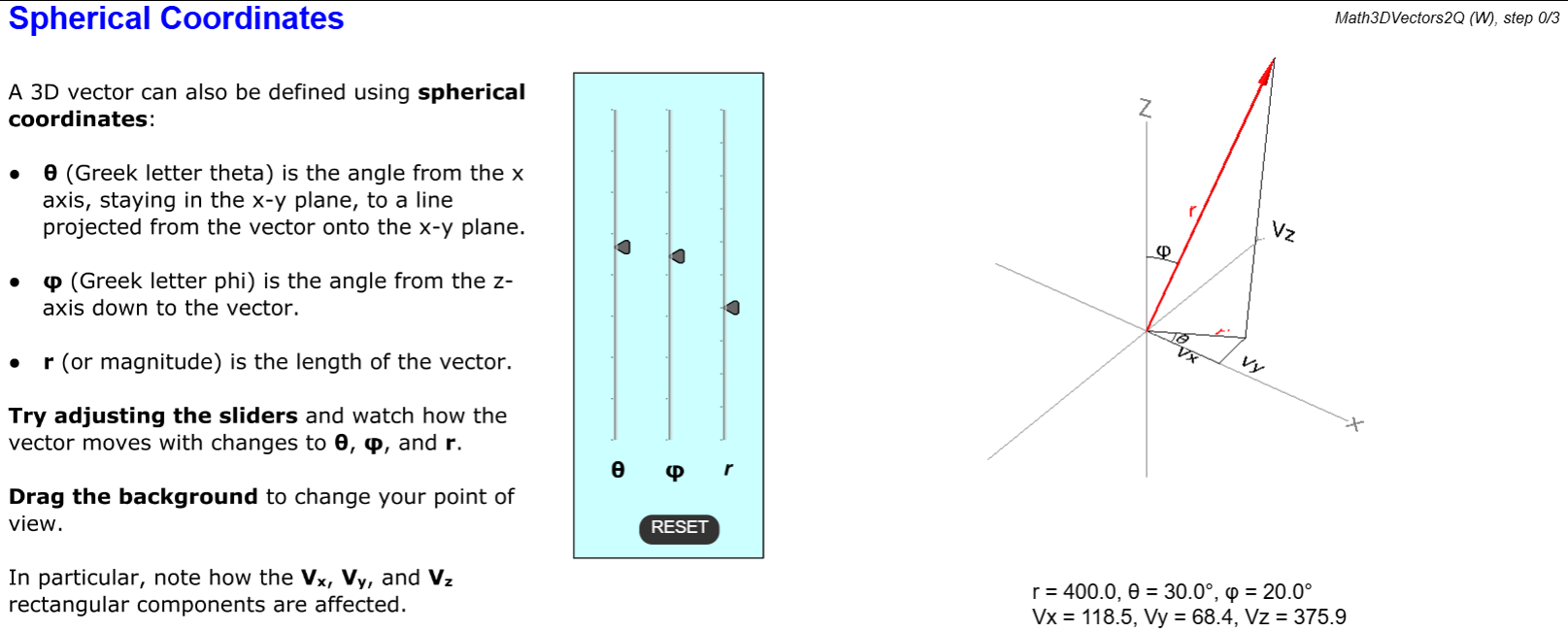
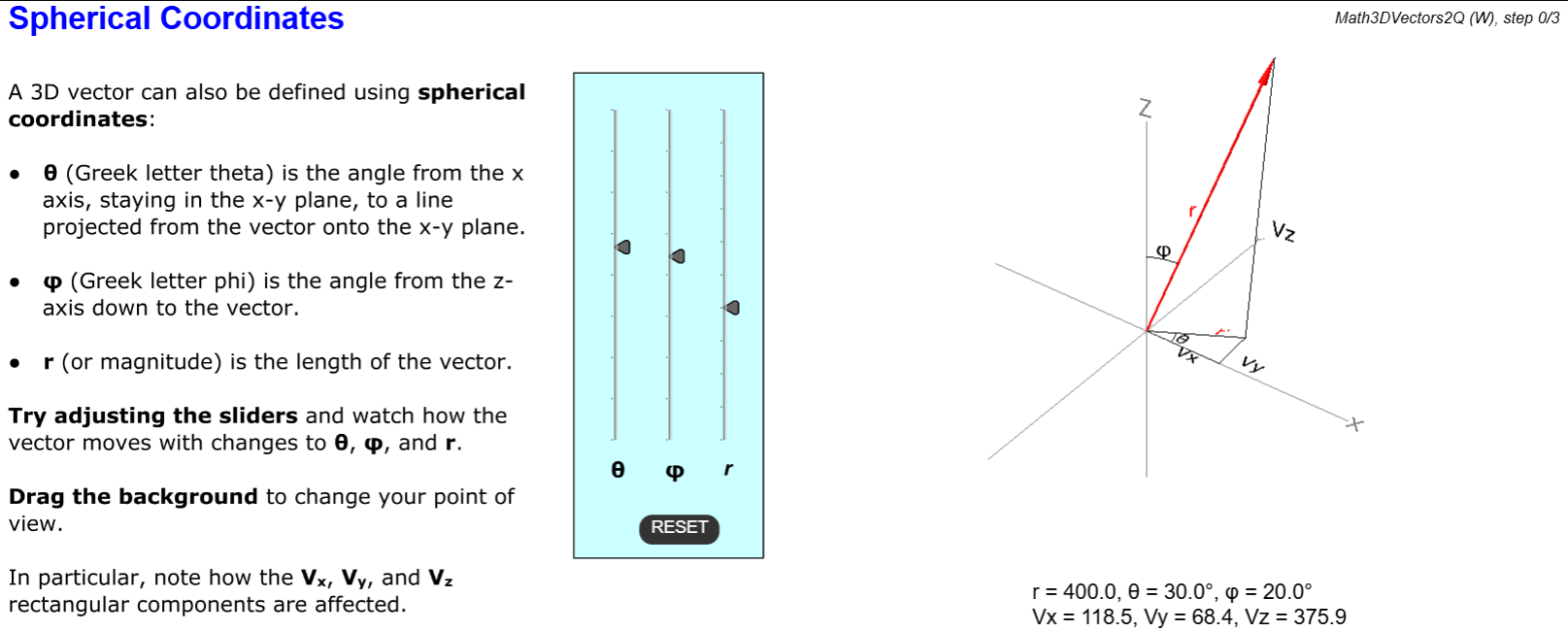
- Vectors
Vector analysis is an integral part of communications engineering. In this lesson we will review: What is a vector? The difference between scalars and vectors. Adding and subtracting vectors. Three-dimensional vectors. Rectangular and spherical coordinates. The vector dot product. The vector cross product.
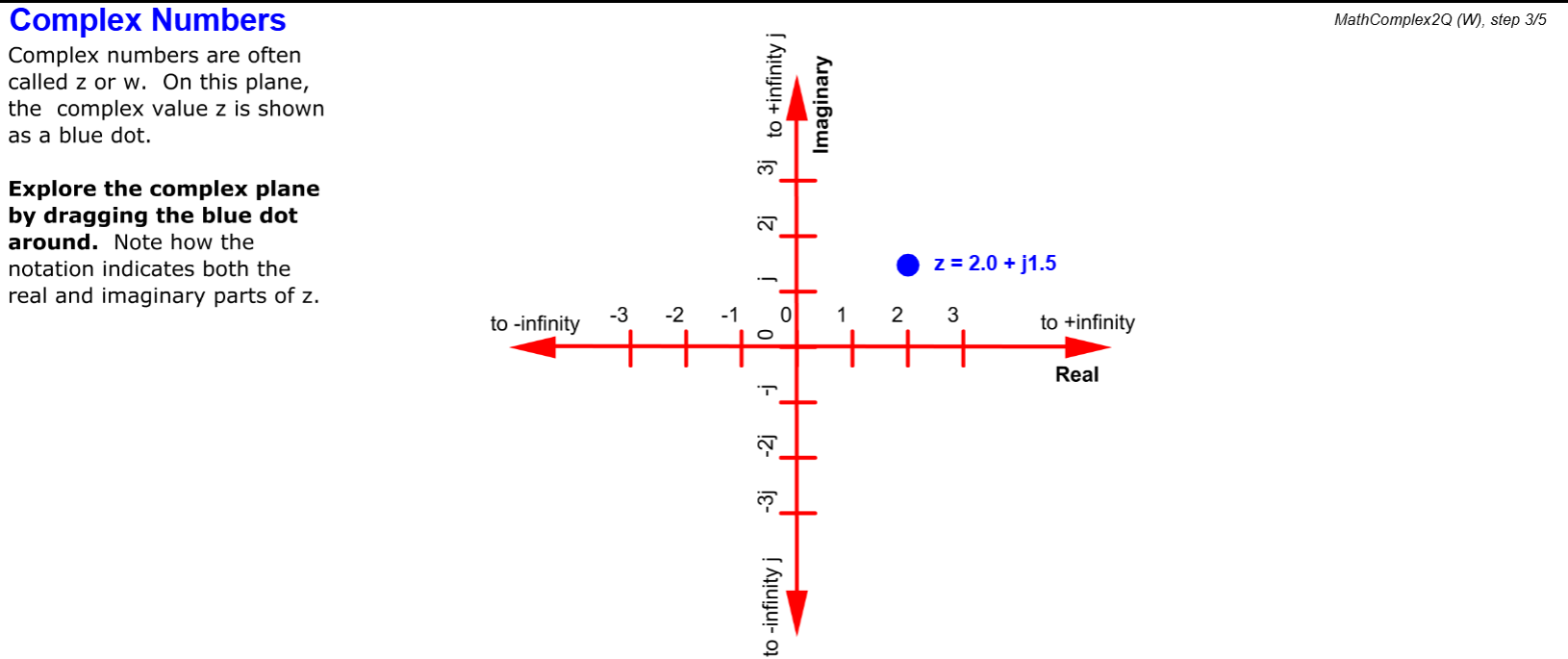
- Complex Numbers
Although complex number theory was first developed in the 1700s, it was its use in the 20th century for digital communications that enabled the satellite and mobile revolution. In this lesson we will review: What is j (or i), the square root of -1? Real, imaginary, and complex numbers. Rectangular and polar notation. Phasors. Euler's Identity and Formula. Complex arithmetic. Complex operations.
- Fourier Transforms
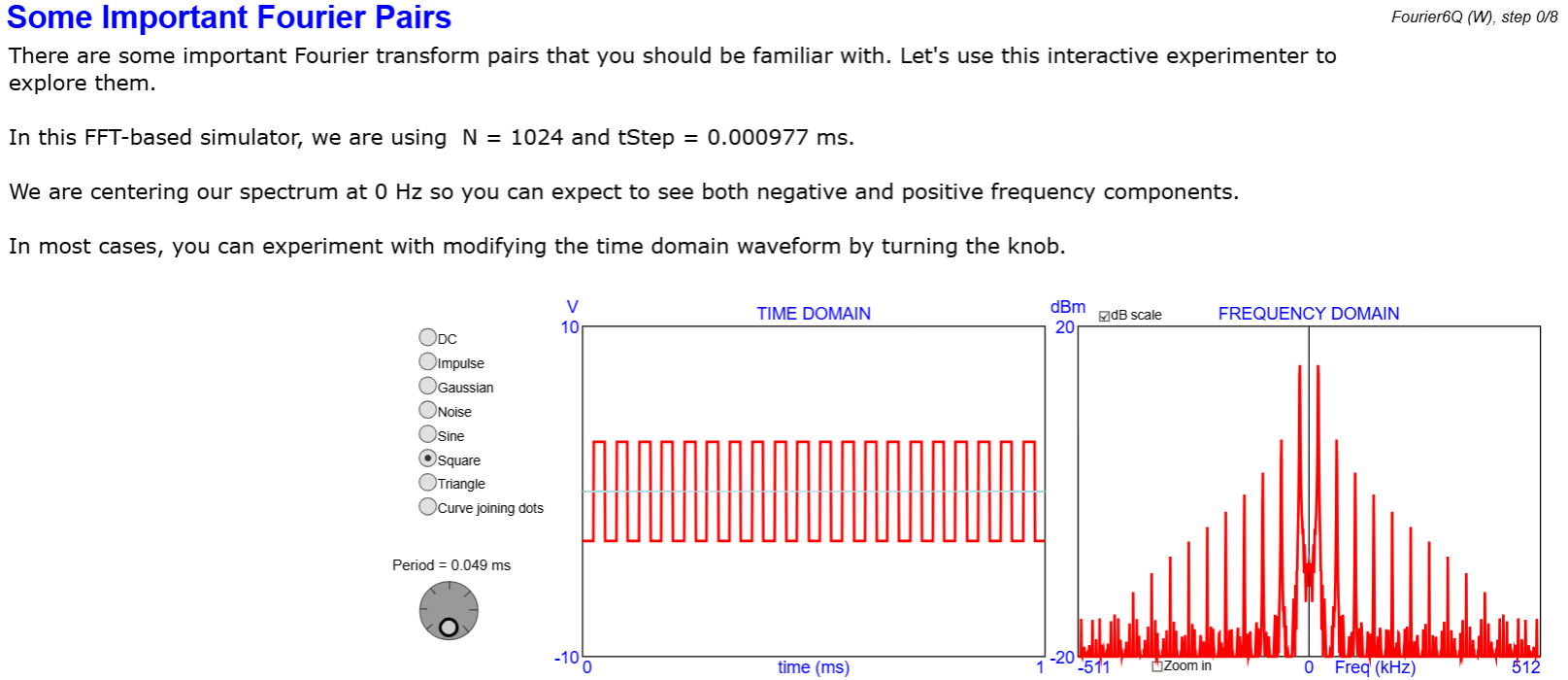
Frequency domain analysis in the complex domain underpins modern signal theory. The Fourier Transform is the most well-known conversion between time domain and frequency domain representation of signals. In this lesson we will review: Time and frequency domain;The Fourier Transform; Fourier Transform formulas;Time/frequency domain duality; DFT and FFT; Important Fourier Transform pairs.
- Spherical Trigonometry
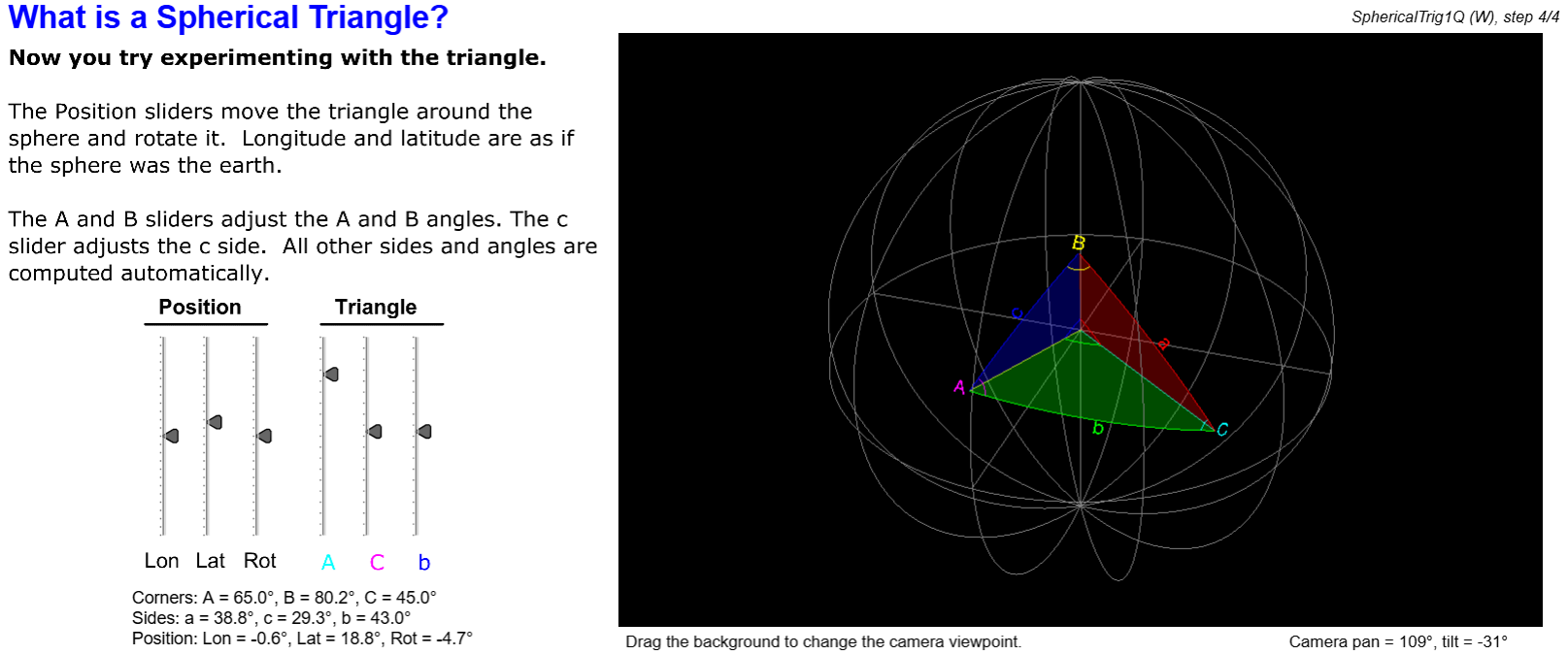
When triangles are wrapped onto the surface of a sphere, the rules of trigonometry are different. Familiarity with spherical trigonometry is important for analyzing problems such as orbits and antenna pointing directions. In this lesson we will review: What is a spherical triangle? Primary formulas: the Rule of Sines and the Rule of Cosines. Formulas for right triangles. Finding the Great Circle distance. Other applications of spherical trigonometry.
 Online Training
Online Training